Canard Aerodynamics

Canard Aerodynamics

We are currently working on a 60° delta wing canard.

The aerodynamic characteristics of the delta wing depend on the free stream velocity and the angle of attack.

The velocity characteristics are usefully divided into low speed (incompressible), medium speed (compressible), transonic, and supersonic flow.

At sufficiently low angles of attack, often linear theory is sufficient. For high angles of attack either experimental data or computational fluid dynamics must be used.

Low speeds, Incompressible flow7687

Lift Coefficient at low speeds

At low speeds and low angles of attack, the suction analogy of Polhamus can be used [1][2].

For higher angles of attack simple theories don't provide accurate values. For our initial attempt we will look for experimental data to apply [3].

Theory of Polhamus

For angles of attack less than about 20° the lift coefficient is aproximated by a fairly simple expression

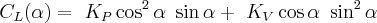
$C_L(\alpha) = \ K_P \cos^2{\alpha}\ \sin{\alpha} +\ K_V \cos{\alpha}\ \sin^2{\alpha}$

Where (α) is the angle of attack in radians.

The constants (K_P) and (K_V) are lift and suction coefficients respectively derived from linear lifting surface theory. For our purposes we can get them from reference [1] page 12.

Since ours is a 60° delta wing, our aspect ratio (AR) is

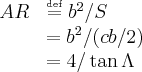
$\begin{array}{ll}\ AR &\overset{\underset{\mathrm{def}}{}}{=} b^2/S\\\ &= b^2/(c b/2)\\\ &= 4/\tan{\Lambda}\ \end{array}$

Where (b) is the length of the root chord, (c) is the maximum wing span, and (S) is the total wing surface area, and (Λ) is the leading edge sweep angle as defined for the arrow wing below.

For the present case of a 60° delta wing our aspect ratio is ~2.31 and a reasonable approximation is (K_P = 2.45) and (K_V = 3.21)

Aerodynamic Center at low speeds

As a very rough approximation the aerodynamic center of a delta wing in incompressible flow is located at 50% of the root chord. The aerodynamic center will typically shift backwards slightly with increasing angle of attack shifting a total of about 4% when the angle of attack reaches of order 20°.

The aerodynamic center will remain near 50% of the root chord until the Mach number nears about 0.8, at which point, assuming reasonably low angles of attack, it should gradually shift toward the supersonic position in a reasonably smooth manner.

Medium speeds, Compressible flow

In many cases compressible flow can computed from incompressible flow using an approximate scaling law such as Prandtl-Glauert or Göthert similarity.

Transonic flow

Transonic flow is usually more complex analytically. Initially we will look for experimental data.

Supersonic flow

Lift Coefficient at supersonic speeds

For low angles of attack there is an exact linear theory [4].

For higher angles of attack, initially we can look for experimental data. However, higher angles of attack may not be too useful initially because the higher forces per angle at supersonic speeds may restrict our control envelope to low angles of attack anyway.

Restating the formula given in reference [4]

The arrow wing is a slight generalization of the delta wing geometry

The parameter (ζ) shown in the diagram is the notch ratio of the arrow wing.

For supersonic flow with a subsonic leading edge, the lift coefficient is given by

$\beta \, C_{L_\alpha} = \ \frac{4m}{E'(m)}\ \left [\frac{\zeta}{1+\zeta}+\ \frac{1-\zeta}{(1-\zeta^2)^{3/2}}\ \cos^{-1}(-\zeta)\ \right ], \qquad m \le 1$

For supersonic flow with a supersonic leading edge, the relation is

$\beta \, C_{L_\alpha} = \ \frac{8m}{\pi(1+\zeta)}\ \left [\frac{1}{\sqrt{m^2-\zeta^2}}\ \cos^{-1}\left ( -\frac{\zeta}{m} \right )\ + \frac{\zeta}{\sqrt{m^2-1}} \cos^{-1}\left ( \frac{1}{m} \right ) \right ], \qquad m \ge 1$

Where for Mach number (M)

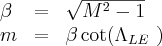
$\begin{array}{lcl}\ \beta &= &\sqrt{M^2-1}\\\ m &= &\beta \cot( \Lambda_{LE}\ ) \end{array}$

Aerodynamic center at supersonic speeds

As a rule of thumb the aerodynamic center for low angles of attack in supersonic flow assuming thin wings is located at 50% of the mean chord. Accounting for the triangular shape of the delta wing this means that the approximate location of the aerodynamic center for our supersonic canard is at 2/3 of the root chord. This result should reasonably accurate for small angles of attack and Mach numbers of 1.1 or greater.

Numeric Examples

The PSAS LV2c rollcontrol fins are 30 degree right triangle half-delta wings with a root chord length of 2.5 inches. What is the lift produced by these fins at Mach 1.1, at 5000 feet altitude, with a fin deflection of 1 degree?

Calculate the lift coefficient for a full 60 degree delta wing, which would be two of our rollcontrol fins. Ignore body interference and boundary layer effects. This is a pretty rough approximation, but serves as a good starting place.

The basic lift formula gives the force perpendicular to the direction of flight (cf. the lift and drag diagram on the CoordinateSystem page)

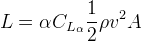
$L = \alpha C_{L_\alpha} \frac{1}{2} \rho v^2 A$

Where (L) is the lift and (α) is the angle of attack.

Using the calculator at http://www.digitaldutch.com/atmoscalc/, at 5000 feet in the standard atmosphere the temperature is 5.1 C, density 1.055 kg/m³, and the speed of sound is 334.4 m/s.

The Mach angle at Mach = 1.1 is

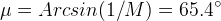
$\mu = Arcsin(1/M) = 65.4^\circ$

This angle is larger than the fin angle, so the rollcontrol fins have a subsonic leading edge, and an (m) value < 1.

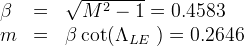
$\begin{array}{lcl}\ \beta &= &\sqrt{M^2-1} = 0.4583\\\ m &= &\beta \cot( \Lambda_{LE}\ ) = 0.2646 \end{array}$

To evaluate CL_α, the elliptic integral E^'(m) must be evaluated. E^'(0) = π/2, for m < 1, a polynomial approximation can be used (See Abramowitz and Stegun [5], 17.3.36. Note that versus Abramowitz and Stegun, m-squared is used in the series here. This is intentional and consistent with the aerodynamic formula given above.)

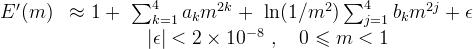
$\begin{array}{lcl}\ E^\prime(m) &\approx 1 +\ \sum_{k=1}^4 a_k m^{2k} +\ \ln(1/m^2) \sum_{j=1}^4 b_k m^{2j} + \epsilon\\\ &|\epsilon| < 2 \times 10^{-8}\ , \quad 0 \leqslant m < 1\ \end{array}\$

Where the coefficients are

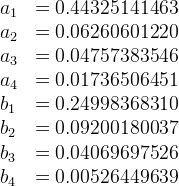
$\begin{array}{lcl}\ a_1 &= 0.44325141463\\\ a_2 &= 0.06260601220\\\ a_3 &= 0.04757383546\\\ a_4 &= 0.01736506451\\\ b_1 &= 0.24998368310\\\ b_2 &= 0.09200180037\\\ b_3 &= 0.04069697526\\\ b_4 &= 0.00526449639\\\ \end{array}$

Applying this approximation to m = 0.2646, yields E^' = 1.079.

The coefficient of lift per alpha can now be calculated using the formula for m < 1. In this example (ζ = 0), so everything in the square brackets evaluates to arcosine(0) = π/2. So

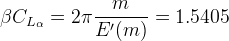
$\beta C_{L_\alpha} = 2 \pi \frac{m}{E^\prime(m)} = 1.5405$

Dividing by (β), the lift coefficient is found to be (C_{L_α} = 3.3616). Taking the fin area as 11.64 cm², which is the area (A) of a single rollcontrol fin, the lift of one fin under the specified conditions is

$\begin{array}{ll} L &= \alpha C_{L_\alpha} \frac{1}{2} \rho v^2 A\\\ &= 0.01745 \cdot 3.3616 \cdot 0.5\ \cdot 1.055 [\rm{\frac{kg}{m^3}}]\\\ &\quad \cdot(1.1 \cdot 334.4 [\rm{\frac{m}{s}}])^2\ \cdot 11.64\times10^{-4} [\rm{m}^2]\\\ &= 4.87 [\rm{N}]\ \end{array}$

References

[1] http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19680022518_1968022518.pdf
Application of the Leading-Edge-Suction Analogy of Vortex Lift to the Drag Due to Lift of Sharp-Edge Delta Wings

[2] http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19670003842_1967003842.pdf
A Concept of the Vortex Lift of Sharp-Edge Delta Wings Based on a Leading-Edge-Suction Analogy

[3] http://www.kfupm.edu.sa/ae/fspub/2006-44asm-saeed-aiaa2006-0063-deltaw.pdf
Contains experimental lift coefficient for 65° delta wing at low speeds and high angles of attack

[4] http://www.aoe.vt.edu/~mason/Mason_f/ConfigAeroSupersonicNotes.pdf
Page 13 has theory on arrow wings at supersonic velocities.

[5] http://en.wikipedia.org/wiki/Abramowitz_and_Stegun