Simple Rocket Science

Simple Rocket Science

Getting Started

Real spaceflight dynamics are complex. There are only a few basic forces involved, but some of them (namely air resistance) are non-conservative and tricky. In order to make a useful, accurate model of spaceflight you have to build a complex numerical approximation. However there is no need to be too complicated too quickly. A great place to start is to find an analytical solution for a rocket, solving for the height it will travel. Put everything in the 'up' axis and ignoring a ton of things will result in an easy place to start.

The Simplest Case

The true simplest case is a point-mass rocket that is in free space with no gravity, air-resistance and has a simplified model of propulsion. Describing this situation mathematically should result in the classic Tsiolkovsky rocket equation.

Rocket in free space

Consider a rocket in free space. There are no external forces. We will be nice and constrain the motion of the rocket in one direction. At some time the rocket starts to eject mass out of one end of the rocket. Through conservation of linear momentum this will propel the rocket forward.

Derivation

The motion of the rocket in our simple case will be determined by Newton's 2^nd law. Usually written as F = ma since we have a variable mass system we use the more general form of

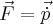
$\vec{F} = \vec{\dot{p}}$

We can safely ignore the vector part because all motion is in one dimension. Also we can re-write p-dot as dp/dt because we are going to use some arguments about infinitesimals to finish our derivation.

$F = \frac{dp}{dt}$

We can write an equation for dp from the diagram below because we know the momentums involved. From the definition of infinitesimal values

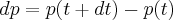
dp = p(t + dt) - p(t)

The momentum at some time plus dt will be the momentum of the rocket plus the momentum of the exhaust gas

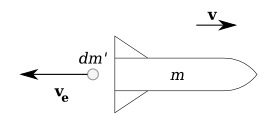
2.2.png

In this diagram you can see we have a rocket of mass m moving at some velocity relative to an inertial reference frame v. At some time t + dt it will release an exhaust mass dm' at some velocity relative to the rocket v_e. Many textbooks refer to v_e as u. In a real rocket is an ideal "effective velocity" of the exit gasses and directly proportional to efficiency of the engine. It is related to the more common term I_sp.

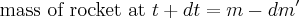
$\mbox{mass of rocket at } t + dt = m - dm^\prime$

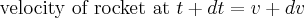
$\mbox{velocity of rocket at } t + dt = v + dv$

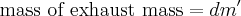
$\mbox{mass of exhaust mass} = dm^\prime$

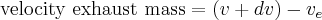
$\mbox{velocity exhaust mass} = (v + dv) - v_e$

Therefore

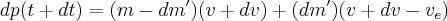
$dp(t + dt) = (m - dm^\prime)(v + dv) + (dm^\prime)(v + dv - v_e)$

p(t) = mv

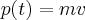
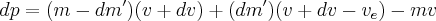
$dp = (m - dm^\prime)(v + dv) + (dm^\prime)(v + dv - v_e) - mv$

Simplifying and throwing out higher order terms will reveal

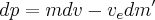
$dp = m dv - v_e dm^\prime$

A positive exhaust mass is a mass lost from the rocket so we say that

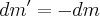
$dm^\prime = - dm$

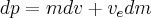
dp = m dv + v_e dm

In this simple case we have no external forces.

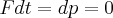
F dt = dp = 0

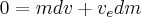
0 = m dv + v_e dm

Solving for dv gives

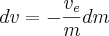
$dv = - \frac{v_e}{m}dm$

We can integrate both sides to find

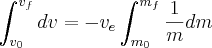
$\int^{v_f}_{v_0}dv = - v_e\int^{m_f}_{m_0}\frac{1}{m}dm$

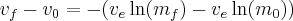
$v_f - v_0 = - (v_e \ln (m_f) - v_e\ln (m_0))$

Simplified this becomes the

Tsiolkovsky rocket equation

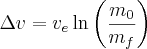
$\Delta v = v_e \ln\left(\frac{m_0}{m_f}\right)$

Since it is hard to look up values of v_e in books about engines we can use its relation to I_sp

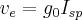
$v_e = g_0 I_{sp}$

Where g₀ is the acceleration due to gravity at the surface of the Earth and I_sp is the specific impulse in seconds.

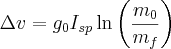
$\Delta v = g_0 I_{sp} \ln\left(\frac{m_0}{m_f}\right)$

Adding Gravity

Starting with our previous result of

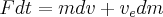
Fdt = m dv + v_e dm

But now having an external force of gravity, mg

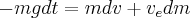
- mgdt = m dv + v_e dm

Solving for dv gives

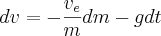
$dv = - \frac{v_e}{m}dm - g dt$

Or as an equation of motion

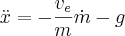
$\ddot x = - \frac{v_e}{m} \dot m - g$

Integrating over v, t and m (Where t_bo is the burn-time of the rocket)

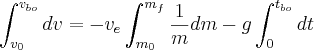
$\int^{v_{bo}}_{v_0}dv = - v_e\int^{m_f}_{m_0}\frac{1}{m}dm - g\int^{t_{bo}}_{0}dt$

Gives an equation for the velocity at burnout

Burnout Velocity

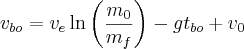
$v_{bo} = v_e \ln\left(\frac{m_0}{m_f}\right) - gt_{bo} + v_0$

The term -gt is referred to as gravity loss. This represents the losses endured by launching in a gravity well. To maximize burnout velocity you want to minimize gravity loss, which means burning the fuel as fast as possible. This makes sense because when you spend a long time burning fuel you are wasting energy lifting unburnt fuel to a higher altitude rather than your payload.

In the real world usually rocket motors are categorized by thrust and not burn time. So it becomes useful to rewrite this equation in terms of a new parameter, thrust-to-weight ratio. We define thrust-to-weight ratio, Ψ, as the thrust (which we assume is constant) divided by the weight at liftoff, m₀g.

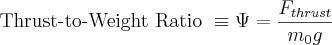
$\mbox{Thrust-to-Weight Ratio } \equiv \Psi = \frac{F_{thrust}}{m_0g}$

If we realize that thrust is

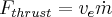
$F_{thrust} = v_e \dot m$

then

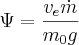
$\Psi = \frac{v_e \dot m}{m_0g}$

We can find a relation to the time it takes to burn through the fuel. If we take the burn rate to be constant (again, not a bad assumption) then the time is to burn out is

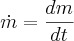
$\dot m = \frac{dm}{dt}$

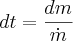
$dt = \frac{dm}{\dot m}$

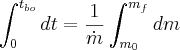
$\int^{t_{bo}}_{0} dt = \frac{1}{\dot m} \int^{m_f}_{m_0} dm$

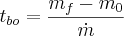
$t_{bo} = \frac{m_f - m_0}{\dot m}$

However we see that m_f - m₀ is negative! This okay because m-dot is secretly also negative. What we actually want is the fuel mass divided by a (positive) burn rate.

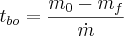
$t_{bo} = \frac{m_0 - m_f}{\dot m}$

We also want this in terms of mass ratio and thrust-to-weight ratio. So we do some clever math, first pulling out m₀

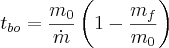
$t_{bo} = \frac{m_0}{\dot m} \left( 1 - \frac{m_f}{m_0} \right)$

Now if we multiply by "one" we get

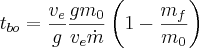
$t_{bo} = \frac{v_e}{g} \frac{g m_0}{v_e \dot m} \left( 1 - \frac{m_f}{m_0} \right)$

We recognize the term 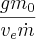$\frac{g m_0}{v_e \dot m}$ as the inverse of Ψ Thus we have the burnout time in reasonably terms

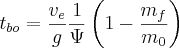
$t_{bo} = \frac{v_e}{g} \frac{1}{\Psi} \left( 1 - \frac{m_f}{m_0} \right)$

Plugging this in for t in our burnout velocity equation gets

$v_{bo} = v_e \left[\ln\left(\frac{m_0}{m_f}\right) - \frac{1}{\Psi} \left( 1 - \frac{m_f}{m_0} \right)\right] + v_0$

Now we can also introduce the symbol μ for the mass ratio (for brevity's sake) and replace v_e with gI_sp

$v_{bo} = g I_{sp} \left[\ln(\mu) - \frac{1}{\Psi} \left( 1 - \frac{1}{\mu} \right)\right] + v_0$

We see now that we have burnout velocity that is in general a function of three parameters: μ, Ψ and I_sp

$v_{bo} (\mu, \Psi, I_{sp})$

Three variables and 3 dimensions is just begging for some graphing. Here is a graph showing the burnout velocity of a vertical rocket at an I_sp of 250 [s]

Burnout Velocities for an Isp of 250. Click to enlarge

You can see that there a heavy dependence on mass ratio. But also to avoid gravity loss it is beneficial to have Ψ as high as you can too. A typical thrust-to-weight ratio is somewhere between 2 and 3 for large commercial rockets.

We can also talk about what effect changing I_sp has on the burnout velocity. If we take the partial with respect to I_sp we get

$\frac{\partial v_{bo}}{\partial I_{sp}} = g \left[\ln(\mu) - \frac{1}{\Psi} \left( 1 - \frac{1}{\mu} \right)\right]$

For a rocket with a μ of 10 and a Ψ of 2 we see that adding an extra second of I_sp results in of 18.2 m/s of extra velocity.

$\frac{\partial v_{bo}}{\partial I_{sp}} = 9.80665 [m/s^2] \left[\ln(10) - \frac{1}{2} \left( 1 - \frac{1}{10} \right)\right] = 18.2 [m/s/s]$

Burnout Height

Now that we have done some work to find the burnout velocity we can find the burnout height much the same way. Starting with our differential equation for rocket motion we double integrate to find range

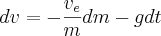
$dv = - \frac{v_e}{m}dm - g dt$

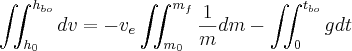
$\iint^{h_{bo}}_{h_0} dv = - v_e \iint^{m_f}_{m_0}\frac{1}{m}dm - \iint^{t_{bo}}_{0}g dt$

I had to look this one up in a table of integrals but the answer should be

$h_{bo} = -v_e \left[ m_f \ln(m_f) - m_f - m_0 \ln(m_0) - m_0 \right] - \frac{1}{2} g t_{bo}^2 + h_0$

This can be rearranged to look like

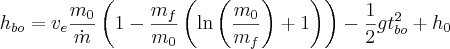
$h_{bo} = v_e \frac{m_0}{\dot m} \left( 1 - \frac{m_f}{m_0} \left( \ln\left(\frac{m_0}{m_f}\right) + 1 \right)\right) - \frac{1}{2} g t_{bo}^2 + h_0$

Doing the same substitution of t and using μ we get

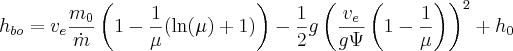
$h_{bo} = v_e \frac{m_0}{\dot m} \left( 1 - \frac{1}{\mu} ( \ln(\mu) + 1)\right) - \frac{1}{2} g \left( \frac{v_e}{g\Psi} \left( 1 - \frac{1}{\mu} \right)\right)^2 + h_0$

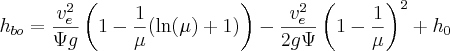
$h_{bo} = \frac{v_e^2}{\Psi g} \left( 1 - \frac{1}{\mu} ( \ln(\mu) + 1)\right) - \frac{v_e^2}{2g\Psi}\left(1 - \frac{1}{\mu}\right)^2 + h_0$

Now making our I_sp substitution

$h_{bo} = \frac{g I_{sp}^2}{\Psi} \left[\left( 1 - \frac{\ln(\mu) + 1}{\mu}\right) - \frac{1}{2}\left(1 - \frac{1}{\mu}\right)^2\right] + h_0$

Ballistic Trajectory

After burnout the rocket will continue to move upwards on a ballistic trajectory. Since we are considering gravity as a constant and ignoring air resistance we can use energy arguments to easily figure out the final height the rocket will go

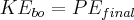
$KE_{bo} = PE_{final}$

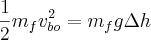
$\frac{1}{2} m_f v_{bo}^2 = m_f g \Delta h$

Solving for the change in height

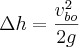
$\Delta h = \frac{v_{bo}^2}{2g}$

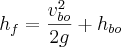
$h_f = \frac{v_{bo}^2}{2g} + h_{bo}$

Bringing it all together

So if we really like math we can combine the ballistic and burnout equations to find the total height a rocket under constant gravity with no air resistance will travel (as a function of μ, Ψ and I_sp)

$h_f = g I_{sp}^2 \left[\frac{1}{2} \left[\ln(\mu) - \frac{1}{\Psi} \left( 1 - \frac{1}{\mu} \right)\right]^2 + \frac{1}{\Psi} \left[\left( 1 - \frac{\ln(\mu) + 1}{\mu}\right) - \frac{1}{2}\left(1 - \frac{1}{\mu}\right)^2\right]\right]$

References

[1] Turner, Martin J.L. Rocket and Spacecraft Propulsion. Springer Praxis Books. [New York]: Praxis Publishing Ltd, Chichester, UK, 2005.

[2] Thomson, William Tyrrell. Introduction to Space Dynamics. New York: Wiley, 1961.