PSAS/ orbit intro

Introduction to Orbits

  1. Introduction to Orbits
    1. What's an Orbit
    2. Gravitational Potential
      1. Earth as a Gravity Well
      2. Escape Velocity
    3. Energy of an Orbit

What's an Orbit

When we talk about objects being in space one often imagines things just float around up there. Popular thinking assumes that if you can just get far enough off the surface of the earth you will be in "space" where there is no gravity. But this is not at all how the universe works. In fact there is a lot of gravity in space — there is gravity everywhere in the universe. In order to orbit the earth an object must do something to counteract gravity. That something is going in a circle around the earth fast enough such that your angular momentum overcomes gravity.

Gravitational Potential

Earth as a Gravity Well

We often use the phrase "gravity well" when describing the gravity of the earth. A well is a good analogy because if you plot the change in gravitational potential energy as a function of altitude you will see two "walls" with the earth at the bottom. We experience this well every time we jump. Jumping converts a small amount of chemical energy in your muscles to kinetic energy, and in accordance with this graph will lift you off the earth some distance. Unfortunately the amount of energy available to us is very small; we are literally stuck at the bottom of the well.

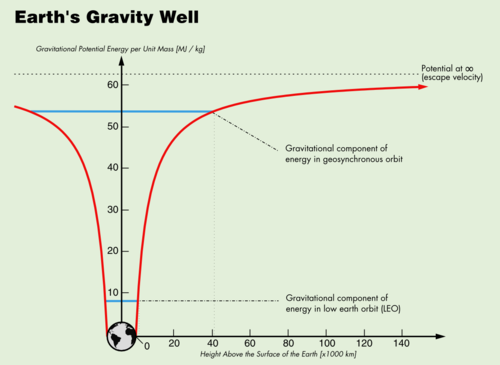Earth's Gravity Well. Click to enlarge

The higher you try to get above the earth's surface, the more energy it is going to take. Thus, without a lot of energy (read: spaceship fuel) you will never get very far off the earth. Worse yet, just getting to a particular height without gaining the necessary tangential velocity for orbiting you will just fall back down to the surface again. That is, unless you go so fast that you "escape" earth's gravity well altogether — represented on the graph by the dotted line at the top.

Escape Velocity

We can calculate the energy necessary to escape earth's gravity well completely. Potential is always represented as a difference, there is nothing like an absolute potential, only the difference between the potential at one location and the potential at another.

Gravitational Potential (Φ):

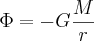
\Phi = -G \frac{M}{r}

There G is the universal gravitational constant; M is the mass of the earth and r is the distance from the center of the earth.

We want to find the difference in potential of an object at infinity (i.e., it has escaped earth forever) and at the surface of the earth. Using r0 as the radius of the earth can write this difference as

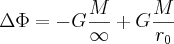
\Delta \Phi = -G \frac{M}{\infty} + G \frac{M}{r_0}

Since the 1/∞ term will go to 0 we find the potential needed to escape earth is

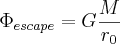
\Phi_{escape} = G \frac{M}{r_0}

Gravitational potential energy is the same as gravitational potential per unit mass. The speed you would need to have enough energy to escape earth's gravity well is called escape velocity To find this number we set the potential energy equal to kinetic energy.

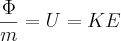
\frac{\Phi}{m} = U = KE

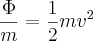
\frac{\Phi}{m} = \frac{1}{2} m v^2

The mass of the object m cancels out as expected because the escape velocity should be the same for all objects. Solving for v we get

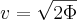
v = \sqrt{2 \Phi}

Substituting our escape potential we get

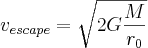
v_{escape} = \sqrt{2 G \frac{M}{r_0}}

Plugging in numbers we find the escape velocity to be 11,181 m/s or about 25,011 mph.

Energy of an Orbit